Steady-State Unconfined Flow with a Seepage Boundary Condition#
Capabilities Tested#
This one-dimensional flow problem tests the Amanzi unsaturated (Richards) flow process kernel with spatially-varying recharge and drain boundary conditions in an unconfined aquifer. Capabilities tested include:
single-phase, one-dimensional flow
steady-state flow
variably-saturated (both saturated and unsaturated) flow
constant-head (Dirichlet) boundary conditions
no-flow (Neumann) boundary conditions
spatially-varying recharge/drain (Cauchy) boundary conditions
homogeneous porous medium
isotropic porous medium
non-uniform, non-orthogonal mesh
For details on this test, see About.
Background#
Unconfined aquifers are often fed by surface recharge (e.g. precipitation), which can be represented in numerical models as a Cauchy boundary condition. Similarly, if the water table intersects the surface topography, perhaps due to slope of the ground surface, a seepage face develops that can likewise be represented with the Cauchy boundary condition.
Flow in an unconfined aquifer is inherently multi-dimensional, which generally precludes simple closed-form analytic solutions. In many practical applications however, vertical gradients and velocities are small relative to their horizontal components and can be neglected following Dupuit [Dup63] and Forchheimer [For30]. The Dupuit-Forchheimer theory of free-surface flow assumes that [FC79]:
flow is horizontal and equipotential lines are vertical, and
hydraulic gradient is equal to the slope of the free surface.
In this problem, we present an analytical solution for the elevation of the water table in an unconfined aquifer where the upper bounds are at once draining along a seepage face and being fed by areal recharge. Analytical solution results are compared to those generated using Amanzi.
Model#
An analytic solution for the elevation of the water table can be readily derived if we make Dupuit-Forchheimer assumptions of free-surface flow — that is, that flow is horizontal and the hydraulic gradient is equal to the slope of the free surface [FC79].
Let \(L_s\) [m] denote the unknown location of the seepline, and \(h_s\) [m] denote the hydraulic head or height of the water table at this location. Between the left boundary and seepline, the analytic solution for hydraulic head in the saturated zone ([Ale07], Equation 4.3.5) \(h\) is analogous to Amanzi unconfined aquifer test case #1 (Steady-State Flow in an Unconfined Aquifer: Head, and Flux Boundary Conditions), with \((L_s,h_s)\) taking the place of \((L,h_L)\):
(1)#\[h^2 = h_0^2 + (h_s^2 - h_0^2) \frac{x}{L_s} + \frac{Q_{src}L_s^2}{K}\left( \frac{x}{L_s} \right) \left(1 - \frac{x}{L_s} \right),\: 0 \leqslant x \leqslant L_s,\]
where \(Q_{src}=-Q\) the seepline is position at \(x=L_s\) [m].
The hydraulic head, \(h\) [m], is also the height of the water table. To the right of the seepline, any surface water is assumed to readily drain off such that the hydraulic head or water table elevation coincides exactly with the ground elevation, that is,
(2)#\[h = 50 \text{ ft} \left(2 - \frac{x}{L} \right),\: L_s \leqslant x \leqslant L\]
The location of the seepline is obtained by recognizing that Darcy’s law and mass conservation across the vertical line \(x=L_s\) requires ([Ale07], Equations 4.4.3 and 4.4.4)
(3)#\[\frac{dh}{dx} \vert_{x=L_s^-} = \frac{1}{h_s} \left[ \frac{h_s^2 - h_0^2}{2L_s} - \frac{Q_{src} L_s}{2K} \right] = \frac{h_L - h_s}{L - L_s} = \frac{dh}{dx} \vert_{x=L_s^+},\]
where
- where
- (4)#\[h_s = 50 \text{ ft} \left(2 - \frac{L_s}{L} \right)\]
Simultaneous solution of Equations (3) and (4) for the specific parameters defined in the test problem schematic yields \(L_s = 829 ft\).
Problem Specification#
Schematic#
Consider the following scenario involving steady-state groundwater flow in an unconfined aquifer that discharges to a sloped ground surface along a seepage face ([Ale07], Section 4.4):
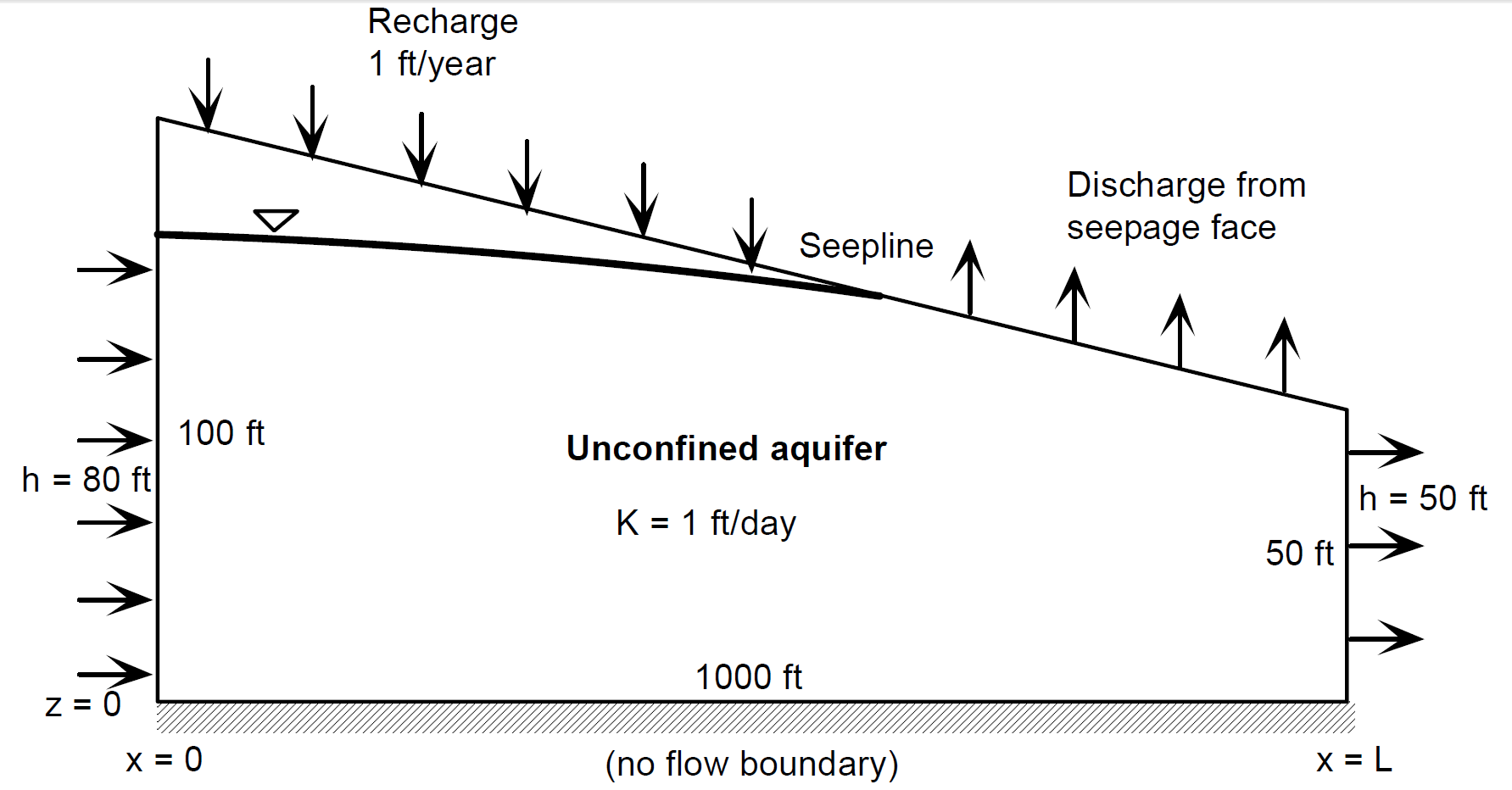
Schematic of the model domain and boundary conditions.#
The ground elevation slopes from 100 ft at \(x=0\) to 50 ft at \(x=L\), and the location of the seepline is unknown a priori.
Mesh#
The mesh uses constant grid discretization in the x-direction (\(\Delta x = 25\) ft) and variable discretization in the y-direction (\(2.5\) ft \(\leqslant \Delta y \leqslant 5\) ft). To conform to the physical domain depicted in the test problem schematic, a conformal grid is used for the Amanzi simulation:
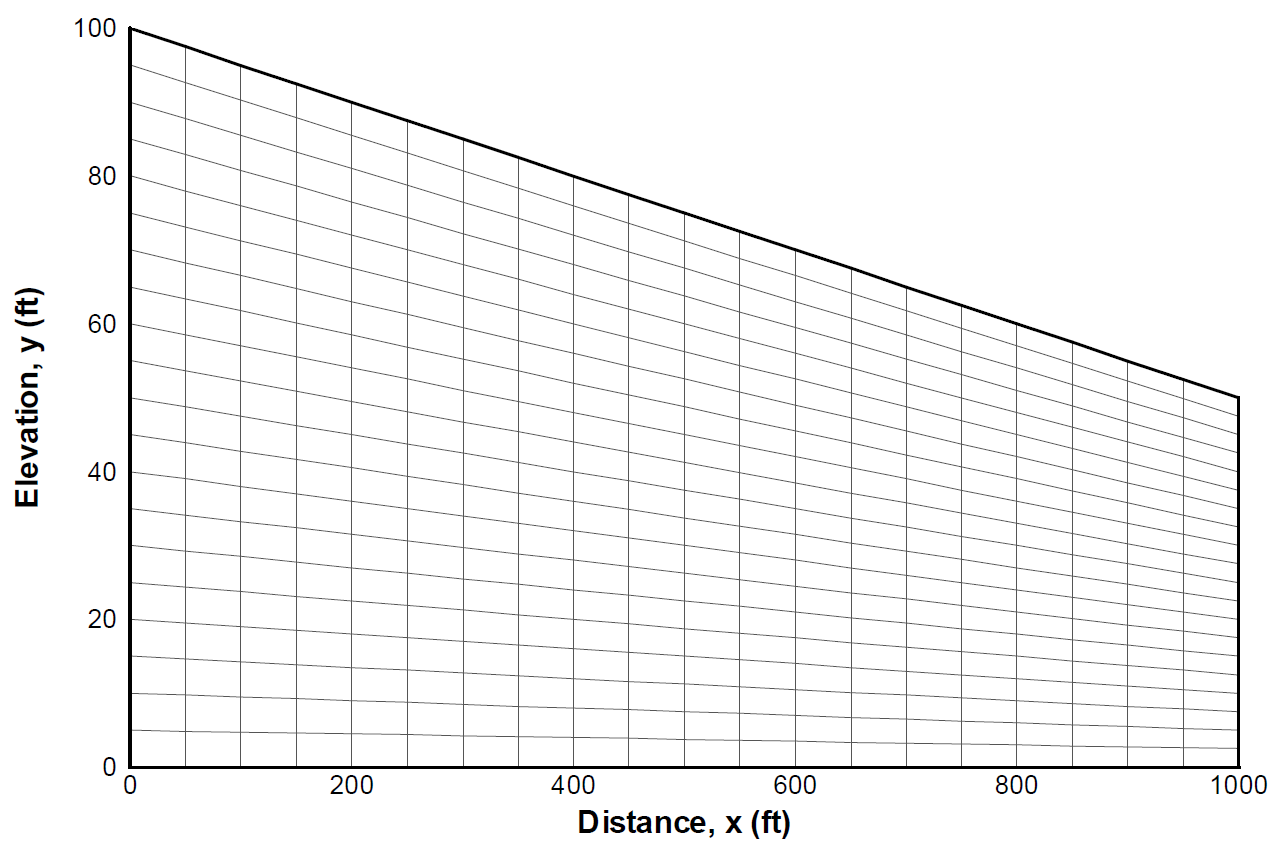
Unstructured two-dimensional mesh with upper bounds conforming to ground surface.#
Variables#
With the Dupuit approximation the analytic solution given by Equation (1) is one-dimensional in the horizontal coordinate and describes only the saturated zone. Because Amanzi does not directly solve a reduced governing equation set based on the Dupuit assumption, a two-dimensional \((x,\,y)\) simulation of the combined saturated and unsaturated zones using the [Ric31] equation is required. Thus a vertical hydraulic conductivity and parameters defining moisture characteristic curves for the unsaturated zone are required beyond the material properties implied by Equation (1). Input parameters for the numerical simulation are summarized as:
Domain (2D)
\(x_{min} = y_{min} = 0 \text{ [ft]}\)
\(x_{max} = L = 1000 \text{ [ft]}\)
\(y_{max} = 100\) at \(x = 0\) and \(50\) at \(x = L \text{ [ft]}\)
Material properties
isotropic hydraulic conductivity: \(K = 1 \text{ [ft/d]} = 3.528 \times 10^{-6} \text{ [m/s]}\)
derived from: \(K=\frac{k \rho g}{\mu}\), where permeability \(k = 3.6098 \times 10^{-13} \text{ [m}^2\text{]}\) (1 ft = 0.3048 m)
porosity: \(\phi = 0.3\)
fluid density: \(\rho = 998.2 \: \text{[kg/m}^3\text{]}\)
dynamic viscosity: \(\mu = 1.002 \times 10^{-3} \: \text{[Pa} \cdot \text{s]}\)
gravitational acceleration: \(g = 9.807 \: \text{[m/s}^2\text{]}\)
van Genuchten [vG80] - Mualem [Mua76] parameters
\(\alpha = 1.0212 \times 10^{-4} \text{ [Pa}^{-1} \text{]}\)
\(S_r = 0.25\)
\(m = 0.09090\)
Boundary conditions
no-flow (Neumann) boundary condition prescribed at \(y_{min}\)
prescribed hydraulic head (Dirichlet): \(h(0) = 80,\: h(L) = 50 \text{ [ft]}\)
recharge along the top surface = 1 ft/y for \(0 \leqslant x \leqslant L_s\)
Results and Comparison#
(Source code, png, hires.png, pdf)
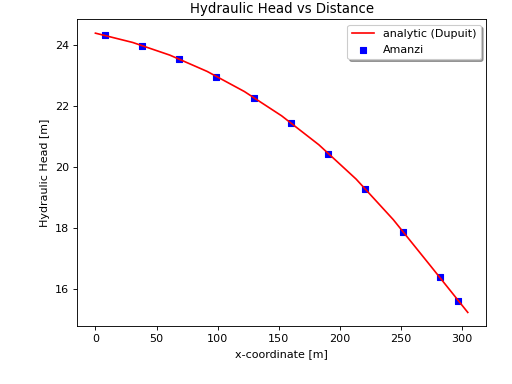
x [m] |
z [m] |
Analytic [m] |
Amanzi [m] |
|---|---|---|---|
7.6 |
0.524 |
24.3183 |
24.3126 |
38.1 |
0.524 |
23.9865 |
23.9714 |
68.6 |
0.524 |
23.5421 |
23.5228 |
99.1 |
0.524 |
22.9784 |
22.9546 |
129.5 |
0.524 |
22.2889 |
22.2572 |
160.0 |
0.524 |
21.4567 |
21.4302 |
190.5 |
0.524 |
20.4667 |
20.4307 |
221.0 |
0.524 |
19.2947 |
19.2685 |
251.5 |
0.524 |
17.9048 |
17.8894 |
282.0 |
0.524 |
16.3800 |
16.3845 |
297.2 |
0.524 |
15.6200 |
15.6238 |
References#
S. Aleman. Porflow testing and verification. Technical Report, Savannah River National Laboratory, 2007.
J. Dupuit. Études théoriques et pratiques sur le mouvement des eaux dans les canaux découverts et à travers les terrains perméables. Dunod, Paris, 1863.
P. Forchheimer. Hydraulik. Teubner, Leipzig, Berlin, third edition, 1930.
R. A. Freeze and J. A. Cherry. Groundwater. Prentice-Hall, Inc., Englewood Cliffs, NJ, 1979.
Y. Mualem. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res, 12(3):513–522, 1976.
L. A. Richards. Capillary conduction of liquids through porous mediums. Physics, 1(5):318–333, 1931.
M.T. van Genuchten. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J, 44(5):892–898, 1980.
About#
Directory: testing/verification/flow/richards/steady-state/unconfined_seepage_1d
Authors: Markus Berndt
Maintainer: David Moulton (moulton@lanl.gov)
Input Files:
amanzi_unconfined_seepage_1d-u.xml (Spec Version 2.3)
mesh: porflow4_4.exo (two-dimensional mesh with conformal (non-orthogonal) grid)
