Steady-State One-Dimensional Flow with Head Boundary Conditions

Capabilities Tested

This one-dimensional, steady-state flow problem tests the Amanzi saturated flow process kernel to simulate flow through a homogeneous, saturated porous medium with constant properties. The analytical solutions for hydraulic head and Darcy velocity can be used to test the Amanzi implementation of prescribed hydraulic head boundary conditions, Darcy’s law [Dar56], and mass conservation for an elementary problem.

Capabilties tested include:

• steady-state, one-dimensional flow

• saturated flow conditions

• constant-head (Dirichlet) boundary conditions

• mass conservation

• exactness of numerical scheme for linear head

• homogeneous porous medium

For details on this test, see About.

Background

For one-dimensional, steady-state, flow through a saturated porous medium with constant properties, the general governing differential equation expressing mass conservation and Darcy’s law [Dar56] becomes simply

(1)\[\frac{d^2h}{dx^2} = 0\]

where the total head (\(h\), [L]) is the sum of pressure head (\(P/\rho g\), [L]) and elevation (\(z\), [L])

\[h = \frac{P}{\rho g}+z\]

\(\rho\) = density [M/L³], \(g\) = gravitational acceleration [L/T²], and \(x\) = horizontal distance [L]. The ordinary differential equation (1) is easily solved by direct integration as

(2)\[h = C_1 x + C_2\]

where the integration constants \(C_1\) and \(C_2\) depend on the boundary conditions.

Analytic solution for prescribed inlet and outlet pressures

Model

The analytic solution for prescribed inlet and outlet pressures is presented below. When hydraulic head is prescribed at both boundaries as

(3)\[\begin{split}h(0) &= h_0\\ h(L) &= h_L\end{split}\]

the analytic solution (2) for hydraulic head becomes

(4)\[h = (h_L - h_0) \frac{x}{L} + h_0\]

where \(L\) = domain length [L]. For these boundary conditions the volumetric flowrate per unit area, or Darcy velocity (\(U\), [L/T]), is defined by Darcy’s law [Dar56] as

(5)\[U = -\frac{k}{\mu}\rho g \frac{dh}{dx} = -K\frac{dh}{dx} = K\frac{h_0 - h_L}{L}\]

where \(k\) = intrinsic permeability [L²], \(\mu\) = viscosity [M/LT], and \(K\) = hydraulic conductivity [L/T].

Amanzi verification test problem

Problem Specification

Schematic

The domain is shown in the following schematic.

One-dimensional, steady-state flow through a saturated porous medium with constant properties.

Mesh

The numerical mesh has dimensions \(100 \: m \times 2 \: m \times 10 \: m\). The mesh is comprised of 20 cells with uniform discretization such that it contains 20 cells in the x-direction, 1 cell in the y-direction, and 1 cell in the z-direction (\(\Delta x = 5 \text{ m}, \: \Delta y = 2 \text{ m}, \: \Delta z = 10 \text{ m}\)).

Variables

To generate numerical results, the following specifications are considered:

• Domain

  • \(x_{min} = y_{min} = z_{min} = 0\)

  • \(x_{max} = 100\) m, \(y_{max} = 2\) m, \(z_{max} = 10\) m

• Horizontal flow in the x-coordinate direction

  • no-flow prescribed at the \(y_{min}, \: y_{max}, \: z_{min}, \: z_{max}\) boundaries

  • prescribed hydraulic head at the x-coordinate boundaries: \(h(0) = 20 \: \text{[m]}, \: h(L) = 19 \: \text{[m]}\)

• Material properties:

  • \(\rho = 998.2 \: \text{[kg/m}^3\text{]}\)

  • \(\mu = 1.002 \times 10^{-3} \: \text{[Pa} \cdot \text{s]}\)

  • \(g = 9.807 \: \text{[m/s}^2\text{]}\)

  • \(K = 1.0 \: \text{[m/d]}\) (permeability: \(k = 1.1847 \times 10^{-12} \text{ [m}^2\text{]})\)

For these input specifications, Amanzi simulation output is expected to closely match

(6)\[h = 20 -\frac{x}{100} \text{ [m]}\]

and

(7)\[U = 1.0 \text{ [m/d]}\]

following Equations (4) and (5).

Results and Comparison

The discretization is exact for linear solutions, and it is clear in the figure that Amanzi has reproduced the exact solution. On the boundary Amanzi takes the head value from a nearby cell. This could be fixed in the future.

(Source code, png, hires.png, pdf)

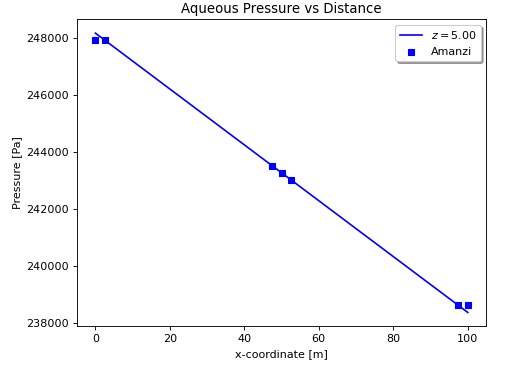
This is also visible in the following table:

x [m]	z [m]	Analytic [Pa]	Amanzi [Pa]
0.0	5.0	248159.9704	247915.2455
2.5	5.0	247915.2455	247915.2455
47.5	5.0	243510.1964	243510.1964
50.0	5.0	243265.4714	243265.4714
52.5	5.0	243020.7465	243020.7465
97.5	5.0	238615.6974	238615.6974
100.0	5.0	238370.9724	238615.6974

References

Dar56(1,2,3)

H. Darcy. Les fontaines publiques de la ville de Dijon: exposition et application des principes a suivre et des formules a employer. Dalmont, 1856.

About

• Directory: test_suites/verification/flow/saturated/steady-state/linear_head_head_1d

• Authors: Greg Flach, Konstantin Lipnikov

• Maintainer(s): David Moulton, moulton@lanl.gov

• Input Files:

  • amanzi_linear_head_head_1d-s.xml

    • Spec Version 2.3.0, structured mesh framework

    • mesh: steady-flow_mesh.h5

  • amanzi_linear_head_head_1d-u.xml

    • Spec Version 2.3.0, unstructured mesh framework

    • mesh: generated internally

• Mesh Files:

  • steady-flow_mesh.h5

• Analytic solution computed with golden output

  • Subdirectory: golden_output

  • Input Files:

    • steady-flow_data.h5