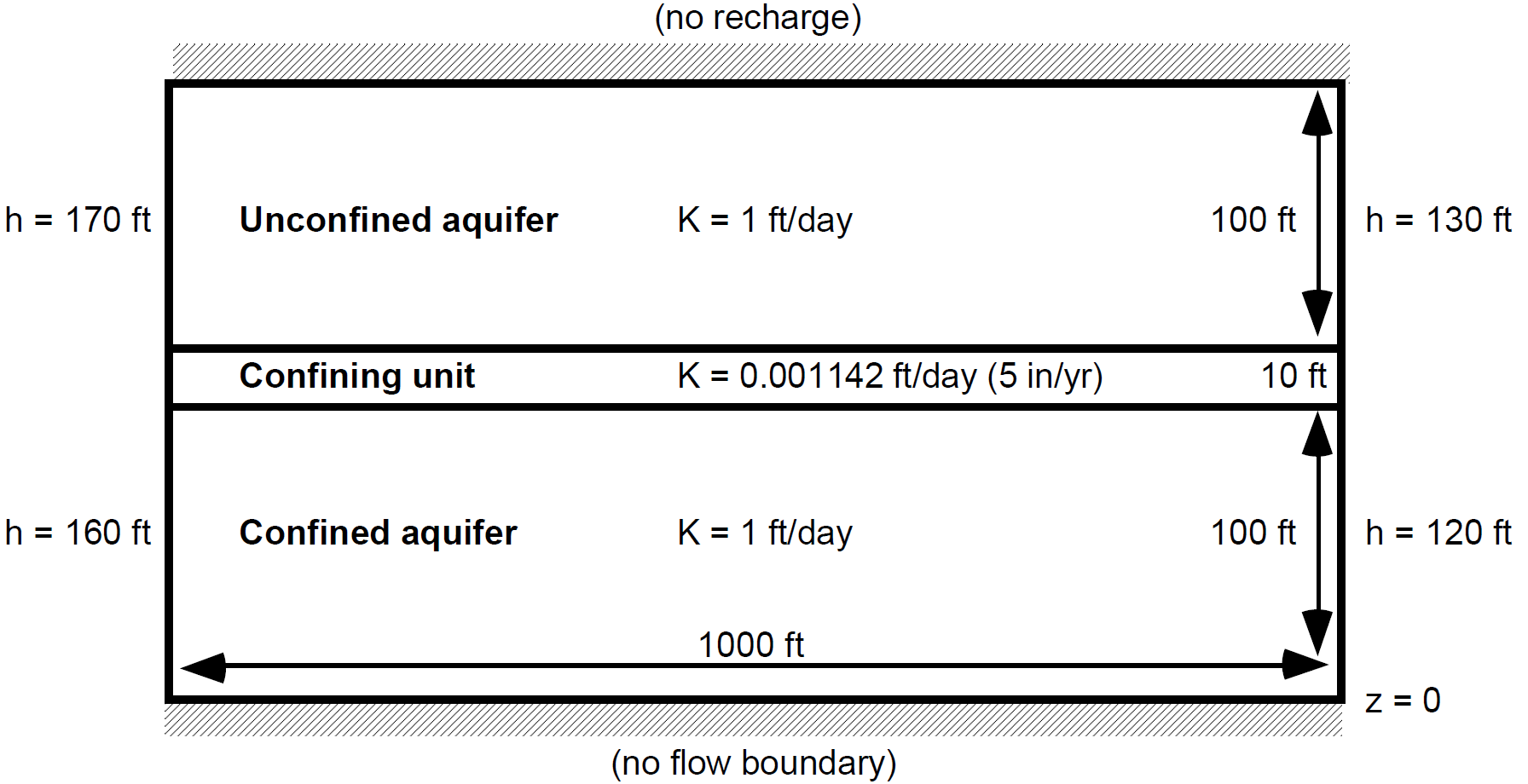
Steady-State Flow in an Unconfined Multi-Aquifer System#
Consider the following scenario involving steady-state groundwater flow through a layered aquifer-aquitard-aquifer system presented by Aleman (2007, Section 4.3):
The scenario combines elements of individual confined and unconfined aquifer test cases for Amanzi, and presents an opportunity to verify that Amanzi can correctly simulate two-dimensional variably-saturated flow through a heterogeneous hydraulic conductivity field (layered system). The test parameters were carefully chosen to enable analytic solution. Specifically, the boundary conditions and conductivity field were chosen to create two aquifers with a nearly constant hydraulic head difference. A constant head difference coupled with a uniform conductivity in the confining unit yields uniform leakance between the two aquifers. Assuming flow in the aquifers is practically horizontal (Dupuit assumption), analytical solutions can be derived for both the unconfined and confined aquifer zones because the source/sink term is spatially constant.
The analytic solution for hydraulic head in the unconfined aquifer is the same as Amanzi unconfined aquifer test case #1 (Aleman 2007, Equation 4.3.5; <link to unconfined test case>)
(1)#\[h^2 = h_0^2 + (h_L^2 - h_0^2) \frac{x}{L} + \frac{Q_{src}L^2}{K}\left( \frac{x}{L} \right) \left(1 - \frac{x}{L} \right)\]
Note: here \(h\) is the elevation above the top of the confining unit. Invoking the Dupuit assumption in the confined aquifer and assuming uniform aquifer thickness, constant properties, and steady-state flow yields the following ordinary differential equation for hydraulic head (e.g. Aleman 2007, Equation 4.3.7; de Marsily 1986)
(2)#\[\frac{d^2h}{dx^2} = \frac{Q}{Kb}\]
where \(b\) = aquifer thickness [L]. For the boundary conditions
(3)#\[\begin{split}h(0) &= h_0\\ h(L) &= h_L\end{split}\]
the analytic solution to ordinary differential equation (2) is
(4)#\[h = h_0 \left( 1 - \frac{x}{L} \right) + h_L \left( \frac{x}{L} \right) + \frac{Q_{src}L^2}{2Kb}\left( \frac{x}{L} \right) \left(1 - \frac{x}{L} \right)\]
Equations (1) and (4) define the hydraulic head variations expected of Amanzi in the unconfined and confined aquifers, respectively.
Aleman, S. 2007. PORFLOW Testing and Verification Document. Savannah River National Laboratory technical report WSRC-STI-2007-00150 Rev 0. 193 p.
de Marsily, G. 1986. Quantitative Hydrogeology: Groundwater Hydrology for Engineers, Academic Press, Inc., Orlando Florida.
Dupuit, J. 1863. Estudes Thèoriques et Pratiques sur le mouvement des Eaux dans les canaux dècouverts et à travers les terrains permèables (Second Edition ed.). Paris: Dunod.
Amanzi verification test problem#
With the Dupuit approximation the analytic solution given by Equation (1) is one-dimensional in the horizontal coordinate and describes only the saturated zone. Because Amanzi does not directly solve a reduced governing equation set based on the Dupuit assumption, a two-dimensional \((x,z)\) simulation of the combined saturated and unsaturated zones using the Richards (1931) equation is required. Thus a vertical hydraulic conductivity and parameters defining moisture characteristic curves for the unsaturated zone are required beyond the material properties implied by Equation (1). To minimize vertical gradients consistent with the Dupuit assumption, the vertical hydraulic conductivity is set 10x higher than the horizontal conductivity in aquifers. Conversely, the horizontal conductivity is set 10x lower than the vertical conductivity in the confining unit. To minimize non-vertical flow in the unsaturated zone, van Genuchten (1980) - Mualem (1976) parameters consistent with a gravel are selected. Input parameters for the numerical simulation are summarized as:
Domain (2D)
\(x_{min} = z_{min} = 0\)
\(x_{max} = L = 1000 ft\), \(z_{max} = 110 ft\)
confined aquifer thickness, \(b = 100 ft\)
confining unit thickness = \(10 ft\)
unconfined aquifer zone thickness = \(100 ft\)
Boundary conditions
no-flow prescribed at the \(z_{min}, z_{max}\) boundaries
no-flow prescribed at \(x_{min}, x_{max}\) for confining unit
prescribed hydraulic head at the x-coordinate boundaries
confined aquifer: \(h(0) = 160 ft, h(L) = 120 ft\)
unconfined aquifer: \(h(0) = 170 ft, h(L) = 130 ft\)
Material properties
\(\rho = 998.2 \: kg/m^3, \mu = 1.002 \cdot 10^{-3} \: Pa\cdot s, g = 9.807 \: m/s^2\)
Hydraulic conductivities
confined aquifer: \(K_{xx} = 1 ft/d\), \(K_{zz} = 10 \, K_{xx}\)
confining unit: \(K_{zz} = 0.001142 ft/d\), \(K_{xx} = K_{zz}/10\)
unconfined aquifer: \(K_{xx} = 1 ft/d\), \(K_{zz} = 10 \, K_{xx}\)
van Genuchten (1980) - Mualem (1976) parameters for a gravel based on Phifer et al. (2006):
\(\alpha = 0.143 cm^{-1} (1.46\cdot 10^{-3} Pa^{-1})\)
\(S_r = 0.052\)
\(m = 0.314\)
Model discretization
\(\Delta x = 20 ft, \Delta z = 2 ft\)
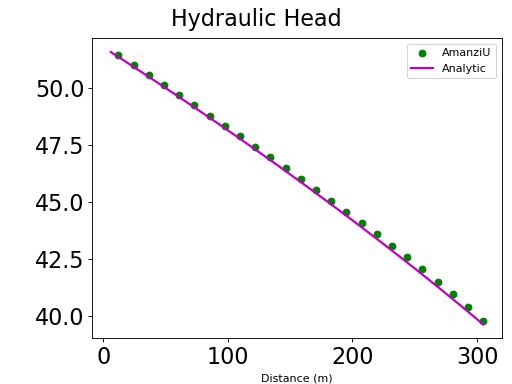
Results and Comparisons#
Results show good match with the semi-analytic solution.
(Source code, png, hires.png, pdf)
References#
Mualem, Y. 1976. A new model predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12:513-522.
Phifer, M. A., M. R. Millings, and G. P. Flach. 2006. Hydraulic Property Data Package for the E-Area and Z-Area Soils, Cementitious Materials, and Waste Zones. Savannah River National Laboratory technical report WSRC-STI-2006-00198 Rev 0. 325 p.
Richards, L.A. 1931. Capillary conduction of liquids through porous mediums. Physics 1 (5): 318-333.
van Genuchten, M. Th. 1980. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 44: 892-898.
Todo
insert table comparing analytic and Amanzi hydraulic heads