Transient Flow in a 2D Confined Aquifer with a Disc Embedded in A Matrix#
Capabilities Tested#
This transient two-dimensional flow problem — with a constant pumping rate in a heterogenous confined aquifer — tests the Amanzi saturated flow process kernel. Capabilities tested include:
single-phase, two-dimensional flow
transient flow
saturated flow
constant-rate pumping well
constant-head (Dirichlet) boundary conditions
heterogeneous isotropic porous medium
uniform mesh
For details on this test, see About.
Background#
Butler and Liu [BL93] developed a semi-analytical solution for calculating drawdown in an aquifer system, in which a disc of one material is embedded in a matrix of different hydraulic properties. The problem is interested in drawdown as a function of location and time due to pumping from a fully penetrating well located either in the disc or the matrix. The differences in hydraulic properties between the disc and the matrix can be of any magnitude. The problem is solved analytically in Laplace space and the drawdown is solved numerically by inversion from the Laplace space to the real space.
Model#
Flow within the circular disc (\(i =1\)) and surrounding matrix (\(i =2\)) can be described mathematically by the polar-coordinate form of groundwater flow equations:
where \(s_i\) is the drawdown [L] in material \(i\), \(t\) is the time [T], \(T_i\) is the transmissivity [L2/T] of material \(i\), and \(S_i\) is the storage coefficient [-] of material \(i\).
The initial conditions are the same for the disc and the matrix:
The boundary condition at infinite distance is:
A pumping well discharging at a constant rate \(Q\) [L3/T] is assumed at location \((r_{pw}, \theta_{pw})\)
where \(R\) is the distance between the pumping and observation wells. To ensure flow continuity, the auxiliary conditions at the matrix-disc interfaces (\(r = a\)) must be met:
Problem Specification#
Schematic#
The problem configuration is illustrated in the following schematic figure:
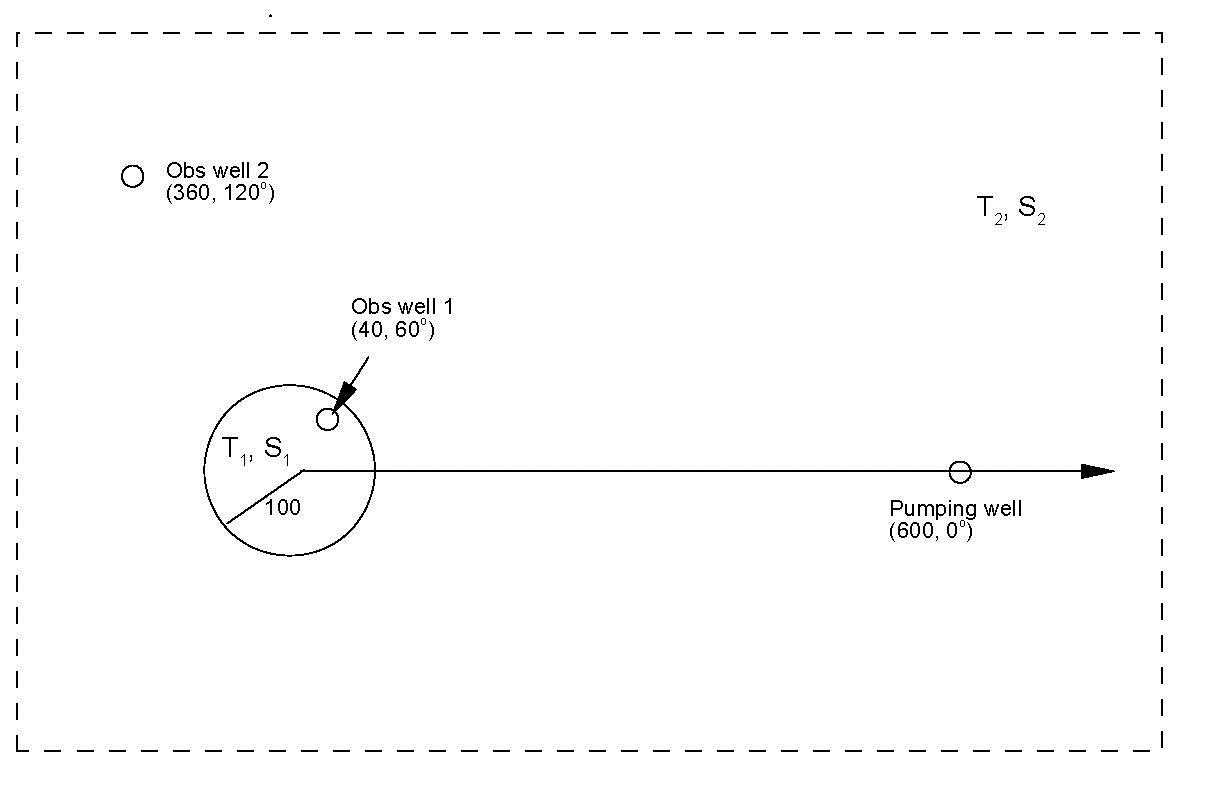
Schematic of the Butler and Liu pod verification problem#
Mesh#
A non-uniform mesh was used to better represent the disc in numerical simulations (Fig. 2), where the central part of the domain is refined to better represent the disc. The grid spacing increases geometrically toward the domain boundaries.
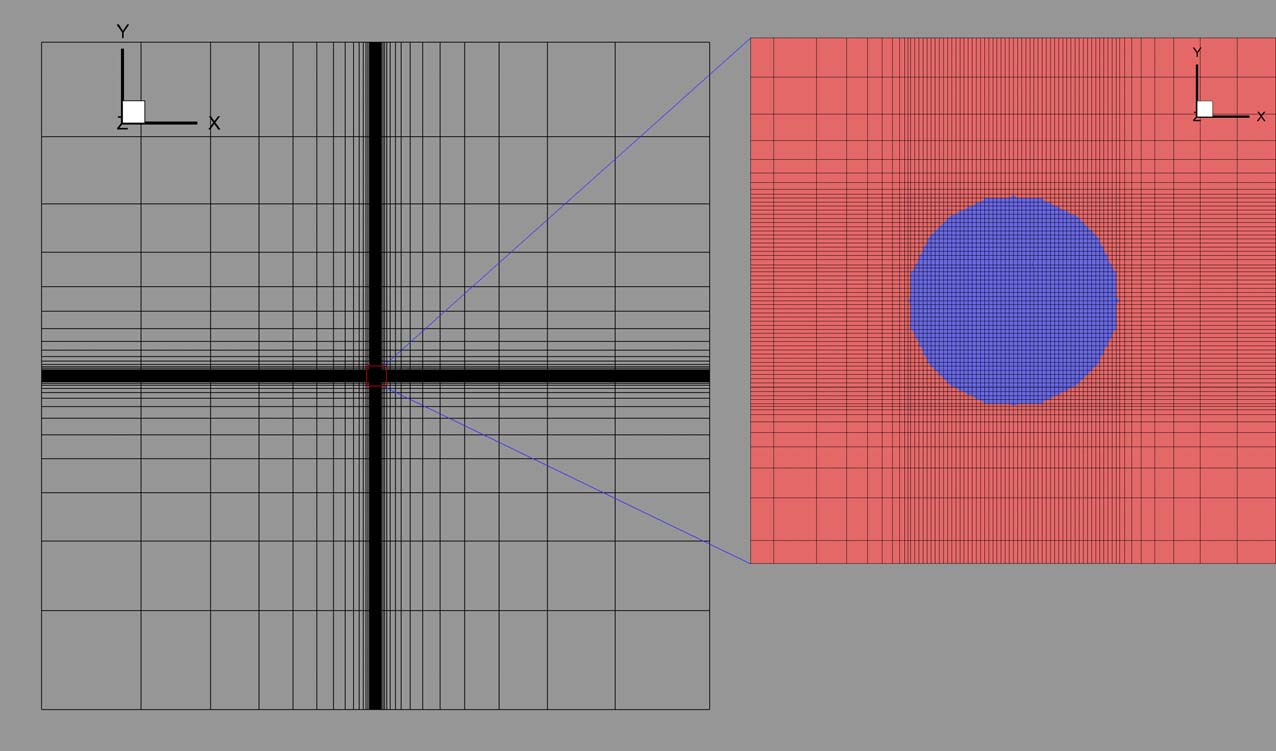
Mesh of the Butler and Liu’s pod verification problem#
Variables#
Domain:
\(x_{min} = y_{min} = z_{min} = 0 \text{ [m]}\) (in mesh/cartesian coordinates)
\(x_{max} = y_{max} = 20200, z_{max} = 1 \text{ [m]}\) (in mesh/cartesian coordinates)
aquifer thickness: \(b=z_{max}-z_{min} = 1 \text{ [m]}\)
pumping well location: \((r_{pw}, \theta_{pw}) = (600 \text{m}, 0^{\circ})\)
observation well locations:
\((r_{obs40},\theta_{obs40}) = (40 \text{m},360^{\circ})\)
\((r_{obs360},\theta_{obs360}) = (60 \text{m},120^{\circ})\)
Material properties:
transmissivity (all isotropic): \(T_1 = 0.0011574 \text{ [m}^2 \text{/s]}\), \(T_2 = 0.011574 \text{ [m}^2 \text{/s]}\), derived from \(T=Kb\), where \(K=\frac{k \rho g}{\mu}\) and intrinsic permeability is \(k_1 = 1.187 \times 10^{-10}, \: k_2 = 1.187 \times 10^{-9} \text{ [m}^2 \text{]}\)
storativity: \(S_1= S_2 = 2.0\times 10^{-4} \: \text{[-]}\), derived from \(S=S_s b\), where \(b=1 \: \text{[m]}\)
porosity: \(\phi_{1,2} = 0.25\)
fluid density: \(\rho = 1000.0 \: \text{[kg/m}^3\text{]}\)
dynamic viscosity: \(\mu = 1.002 \times 10^{-3} \: \text{[Pa} \cdot \text{s]}\)
gravitational acceleration: \(g = 9.807 \: \text{[m/s}^2\text{]}\)
Boundary and initial conditions:
initial condition: \(s(r,\theta,0)=0\)
constant-head (Dirichlet) boundary conditions: \(s(x_{min,max},y_{min,max},z_{min,max},t) = 0 \text{ [m]}\)
well-head pumping rate: \(Q = -11.5485 \text{ [m}^3 \text{/s]} = 1000 \text{ [m}^3 \text{/d]}\)
duration of pumping: \(t_{max} = 31.7 \text{ [y]}\)
Results and Comparison#
Plot Analytic Solution and Amanzi Results#
(Source code, png, hires.png, pdf)
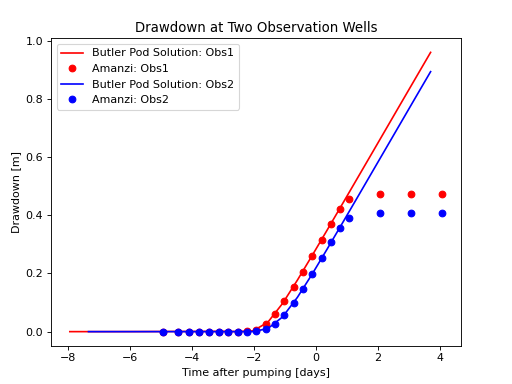
The comparison shows that the results from the Amanzi model match the analytical solution very well at early time, and deviate when the effect of pumping hits the constant head boundary of the domain. Note that the analytical solution was developed for an unbounded domain, so it is therefore expected that the two solutions will deviate from each other at later time. To show that such a deviation is indeed caused by the boundary effect, we also conducted numerical simulations using FEHM, a widely used numerical simulator for simulating heat and mass flow in subsurface environment [ZRDT97]. It is showed that the results from Amanzi are almost the same as those from FEHM, see [LHB14] for detailed comparison.
References#
J. J. Butler and W. Liu. Pumping tests in nonuniform aquifers: the radially asymmetric case. WaterResourcesResearch, 29(2):259–269, 1993.
Z. Lu, D. Harp, and K. Birdsell. Comparison of the amanzi model against analytical solutions and the fehm model. Technical Report, Los Alamos National Laboratory, Los Alamos, NM, 2014.
G. A. Zyvoloski, B. A. Robinson, Z. V. Dash, and L. L. Trease. Summary of the models and methods for the fehm application-a finite-element heat-and mass-transfer code. Technical Report, Los Alamos National Laboratory, Los Alamos, NM, 1997.
About#
Directory: testing/verification/flow/transient/butler_pod_2d
Authors: Zhiming Lu (zhiming@lanl.gov), Dylan Harp (dharp@lanl.gov)
Maintainer(s): Zhiming Lu, Dylan Harp
Input Files:
amanzi_butler_pod_2d-u.xml, Spec, Version 2.3, unstructured mesh framework
mesh_cylinder.exo
Analytical Solutions
Directory: analytic/
Executable: butler_pod.x, compiled from FORTRAN code under the Linux environment.
Input Files:
obs.dat, specifying parameters for observation wells.
anal.dat, specifying other parameters such as the number of timesteps, and so on.
Output Files:
drdn.res, drawdown as a function of time for all observation wells.
Todo
The analytical solution was solved using a FORTRAN code modified from the original code from Greg Ruskauf. We may need to implement the algorithm by ourselves or get permission from Greg Ruskauf for using the code. As the flow problem was solved analytically in the Laplace transformed space, one needs to implement numerical inversion from the Laplace transformed space back to the real space.
