Infiltration 1D#
Capabilities Tested#
partially saturated one-dimensional flow
steady-state flow
pressure and flux boundary conditions
porous medium with discontinuous properties (permeability, van Genuchten parameters)
Background#
Verification problems from the literature have been identified to test isothermal, single-phase, variably saturated flow. We initially focus on test problems that address the two most widely used k-s-p functions, Mualem-van Genuchten [Mua76] [vG80] and Brooks-Corey [BC64]. These include steady-state and transient tests with Dirichlet and Neumann boundary conditions.
This documentation is intended to compare the results from Amanzi against the semi-analytical results documented in “A set of Analytical Benchmarks to Test Numerical Models of Flow and Transport in Soils.” by J. Vanderborght, et. al. http://vzj.geoscienceworld.org/content/4/1/206.abstract [VKH+05], see the first line in Table 3 of that paper. We consider three cases of the steady-state flux in a layered soil profile. The presure profiles should match that in the Vanderborght paper. The difference between the cases is as follows:
case #1 is 0.5 m of clay and 1.5 m of sand;
case #2 is 0.5 m of loam and 1.5 m of sand;
case #3 is 1.5 m of loam and 0.5 m of sand.
Model#
Initial condition. Pressure \(p\) as the function of depths z and time t=0 is 81747 Pa.
Boundary conditions. The pressure at z=0m, the left end in the Figures below, is 99630.6336 Pa. The outflow at the opposite end, z=2m, is fixed at 0.5 cm/d = 5.78703704E-8 m/s.
The absolute permeability tensor is isotropic but discontinuous. The porosity is constant in all tests, \(\phi=0.43\).
Problem Specification#
The problem is solved in a box domain with hight 2 m. The other box dimenstions are equal to 1 m.
Mesh#
We consider a column mesh with 200 cells in the vertical direction.
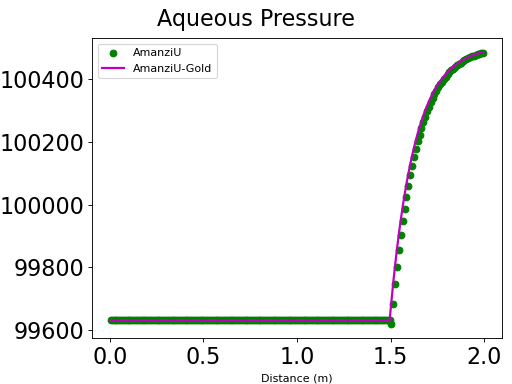
Case #1: Sand Clay Layers#
The steady-state solution is shown below. The sand region corresponds to the left part of the pressure profile. The van Genuchten parameters are \(\alpha=1.532333\cdot 10^{-3}\), \(m=0.6666667\), and residual saturation is \(s_r=0.104651\). The absolute permeability is given by the isotropic tensor \(K=1.18472\cdot 10^{-11} [m^2]\).
The clay region corresponds to the right part of the pressure profile. The van Genuchten parameters are \(\alpha=1.02 \cdot 10^{-4}\), \(m=0.0909\), and residual saturation is \(s_r=0.25\). The absolute permeability is given by the isotropic tensor \(K=1.18\cdot 10^{-13} [m^2]\).
Results and Comparison#
We compare with the Amanzi’s golden data that were verified against the Vanderborght paper.
(Source code, png, hires.png, pdf)
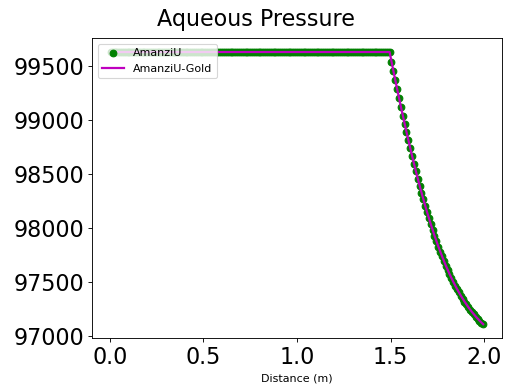
Case #2 Loam Sand Layers#
The steady-state solution is shown below. The sand region corresponds to the left part of the pressure profile. The van Genuchten parameters are \(\alpha=1.532333\cdot 10^{-3}\), \(m=0.6666667\), and residual saturation is \(s_r=0.104651\). The absolute permeability is given by the isotropic tensor \(K=1.18472E-11 [m^2]\).
The loam region corresponds to the right part of the pressure profile. The van Genuchten parameters are \(\alpha=4.08622\cdot 10^{-4}\), \(m=0.375\), and residual saturation is \(s_r=0.186047\). The absolute permeability is given by the isotropic tensor \(K=5.9236 \cdot 10^{-13} [m^2]\).
Results and Comparison#
We compare with the Amanzi’s golden data that were verified against the Vanderborght paper.
(Source code, png, hires.png, pdf)
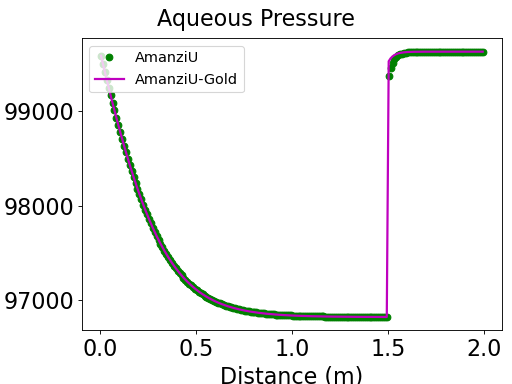
Case #3: Sand Loam Layers#
The steady-state solution is shown below. Now, we swap the sand is loam regions. The van Genuchten parameters are \(\alpha=4.08622\cdot 10^{-4}\), \(m=0.375\), and residual saturation is \(s_r=0.186047\). The absolute permeability is given by the isotropic tensor \(K=5.9236 \cdot 10^{-13} [m^2]\).
The sand region corresponds to the right part of the pressure profile. The van Genuchten parameters are \(\alpha=1.532333\cdot 10^{-3}\), \(m=0.6666667\), and residual saturation is \(s_r=0.104651\). The absolute permeability is given by the isotropic tensor \(K=1.18472 \cdot 10^{-11} [m^2]\).
Results and Comparison#
We compare with the Amanzi’s golden data that were verified against the Vanderborght paper.
(Source code, png, hires.png, pdf)
References#
R.H. Brooks and A.T. Corey. Hydraulic properties of porous media. Hydrology Papers, Colorado State University, 1964.
Y. Mualem. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res, 12(3):513–522, 1976.
M.T. van Genuchten. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J, 44(5):892–898, 1980.
J. Vanderborght, R. Kasteel, M. Herbst, M. Javaux, D. Thiery, M. Vanclooster, C. Mouvet, and H. Vereecken. A set of analytical benchmarks to test numerical models of flow and transport in soils. Vadose Zone J., 4(1):206–221, 2005.
About#
Directory: testing/verification/flow/richards/steady-state/infiltration_1d
Author:
Maintainer: David Moulton (moulton@lanl.gov)
Input Files:
amanzi_infiltration_clay_sand_1d-u.xml
amanzi_infiltration_loam_sand_1d-u.xml
amanzi_infiltration_sand_loam_1d-u.xml
Spec 2.3, unstructured mesh framework
mesh is generated internally
