1D Dispersive Transport with Dual Porosity Model

Capabilties Tested

This one-dimensional transport problem, with a constant contaminant boundary condition and a steady-state flow field, tests the Amanzi transport dual porosity model. Capabilties tested include,

• prescribed constant velocity field

• constant boundary condition for tracer

• advection in an isotropic medium, longitudinal dispersivity

• generalized dual porosity

For details on this test, see About.

Background

This test problem is motivated by confined flow applications with transport from a relatively small source. A typical source would be a well that is fully screened over the confined flow interval. In this case, the steady-state flow field is uniform and the tracer influx does not affect the flow field. The dominant transport processes are advection, dispersion in fractured rock, and solute exchange with immobile fluid in matrix. Matrix play the role of storage and delays propagation of tracer down the flow stream. Dispersion results in the spreading of the released mass in all directions including upstream of the source location. Accuracy of the break-through curve at a distant point down the stream is sensitive to the time step in Amanzi’s operator split approach.

Model

The analytical solution addresses the advection-dispersion equation in the fracture

\[\frac{\partial (\phi_f\, C_f)}{\partial t} = - \boldsymbol{\nabla} \cdot (\boldsymbol{q} C_f) + \boldsymbol{\nabla} \cdot (\phi_f\, (\boldsymbol{D} + \tau_f M) \boldsymbol{\nabla} C_f) - \frac{\phi_m\,\tau_m}{L_m}\, M \nabla C_m,\]

and the linear ODE in the matrix:

\[\frac{\partial (\phi_m\, C_m)}{\partial t} = -\nabla\cdot (\phi_m\, \tau_m\, M \nabla C_m).\]

Here \(\phi\) is porosity, \(\boldsymbol{q}\) is the Darcy velocity, \(\boldsymbol{D}\) is dispersion tensor, \(M\) is molecular diffusion coefficient, and \(L_m\) is the characteristic matrix depth defined typically as the ratio of a matrix block volume to its surface area. Subscripts \(f\) and \(m\) indicate fracture and matrix media, respectively.

We neglect transverse dispersion, so that the dispersion tensor is diagonal:

\[\begin{split}\boldsymbol{D} = \begin{pmatrix} D_{xx} & 0 \\[0.5ex] 0 & D_{yy} \end{pmatrix}, \qquad D_{xx} = \alpha_L v_x, \quad D_{yy} = 0.\end{split}\]

Problem Specification

Schematic

The domain, flow direction, and source location are shown in the schematic below. Note that \(B = L_m\) here.

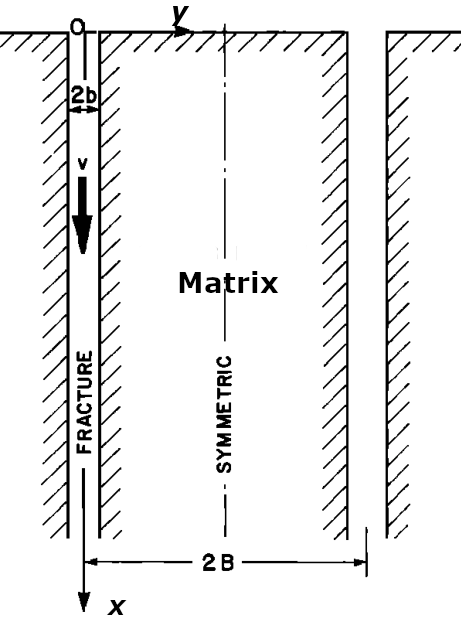
Periodic structure of fractures and matrix.

Mesh

The background mesh consists of square cells with size \(H=1\) m. It has 100 grid cells in the x-direction and 1 grid cell in the y-direction.

Variables

• \(\boldsymbol{q}=(7.922 \cdot 10^{-9},\,0.0)\) constant Darcy velocity [m/s]

• \(\phi_f=0.0001\) constant fracture porosity

• \(\phi_m=0.25\) constant matrix porosity

• \(\alpha_L=1.0\) longitudinal dispersivity [m]

• \(\alpha_T=0.0\) transverse dispersivity [m]

• \(M=2.65 \cdot 10^{-9}\) molecular diffusion coefficient [m^2/s]

• \(\tau_m = 1.0\) matrix tortuosity [-]

• \(\tau_f = 1.0\) fracture tortuosity [-]

• \(L_m = 0.8\) characteristic matrix depth [m]

• \(T=200\) simulation time [y]

Initial condition: \(C_m(x,0)=C_f(x,0) = 0\) [kg/m^3]

Boundary conditions: \(C_f(x,t)=1\) [kg/m^3] at \(x=0.0\) of fracture.

Results and Comparison

The concentrantaion at the fracture end point as the function of time (results are in a good agreement with the analytic solution):

(Source code, png, hires.png, pdf)

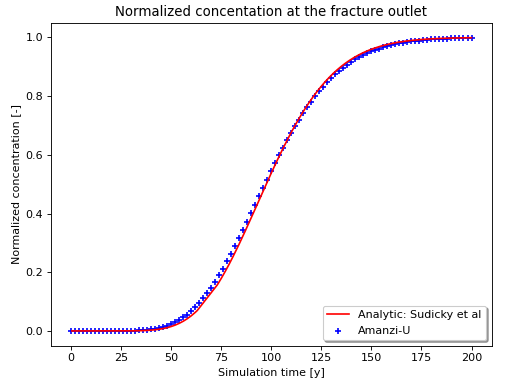
The verification data used in this test is generated from a Fortran code shared by the authors of [].

References

About

• Directory: testing/verification/transport/saturated/transient/dual_porosity_1d

• Authors: Konstantin Lipnikov, David Moulton

• Maintainer(s): Konstantin Lipnikov

• Input Files:

  • amanzi_dual_porosity_1d-u.xml

  • Spec Version 2.3, unstructured mesh framework

• Analytic solution computed with Sudicky’s code:

  • Subdirectory: sudicky

  • Input Files:

    • tracer_conc.txt