Non-grid-aligned transport with calcite precipitation along mixing interface#

Overview and Capabilities tested#

This test example performs the simulation of calcite precipitation in a 2D rectangular flow domain. In this domain, two different solutions are injected at different flow rates at top and bottom half of the inlet face. As a result of the different flow rates, the directions of flow and transport are not aligned with the rectangluar grid, and the mixing zone that develops is curved. Along the curved interface, geochemical disequilibrium drives precipitation of calcite. This example tests the following capabilities:

  • 2D flow

  • 2D advective transport

  • 2D dispersive transport

  • Geochemical reactions

    • Mineral precipitation

For details on this test, see About.

Background#

Mixing-induced precipitation is a problem that has recently received some attention in the literature, especially in pore scale studies [YVWD12], [TRL+08]. To accurately predict precipitation along mixing interfaces, accurate prediction of diffusive transport is required. This is especially true, when these transport processes are not aligned with the grid that is used to discretize the domain. Amanzi uses numerical schemes that accurately simulate non-grid-aligned advective and diffusive transport. In this release, the advection-diffusion equation is solved using an operator splitting framework with an explicit scheme for the advection operator and an implicit scheme for diffusion. A simple operator-split approach is used; future releases will include options for higher-order schemes to couple the processes temporally.

The spatial discretization schemes available in Amanzi for advective and diffusive processes are optimized for the selected mesh framework (structured AMR or unstructured). For unstructured meshes, Amanzi provides a second-order approximation of advective fluxes with a MUSCL-type (Monotonic Upstream-Centered Scheme for Conservation Laws) scheme [Bar94] that combines local linear reconstruction of solute concentrations with a tensorial slope limiter. The tensorial slope limiter adds robustness to the scheme and reduces numerical diffusion compared to the more conventional (scalar) Barth-Jesperson limiter. The tensor diffusion fluxes are computed with either standard central differencing or a second-order MFD (Mimetic Finite Difference) method [dVLM14] optimized to guarantee solution monotonicity. For structured AMR meshes, Amanzi implements an unsplit Godunov scheme [BDS88], [NMAB11] for advection, and a standard 9-point (2D) or 27-point (3D) tensor diffusion scheme. The Godunov scheme robustly guarantees monontonicity for non-grid-aligned advection.

Model#

Flow and transport#

For this test, the domain is fully saturated. The velocity field satisfies the mass conservation equation with a Darcy approximation for volumetric fluxes:

\[\left(\frac{S_s}{g} + \frac{S_y}{Lg}\right) \frac{\partial p}{\partial t} + \boldsymbol{\nabla}\cdot(\rho \boldsymbol{q}) = Q.\]

Solutes are advected with the velocity field given above, and are subject to diffusion fluxes arising from the properties of the solutes in the fluid medium, as well as dispersion terms due to the fluid flow field. The following expresses conservation of the molar density of the i-th solute

\[\frac{\partial (\phi s_l C_i)}{\partial t} + \nabla \cdot \boldsymbol{J}_i^{\text{adv}} = Q_i - \nabla \cdot \boldsymbol{J}_i^{\text{disp}}\]

where the transport flux has the form

\[\boldsymbol{J}_i^\text{disp} = - \phi s_l \boldsymbol{D} \nabla C_i,\]

with the dispersion tensor \(boldsymbol{D}\) and liquid saturation \(s_l\).

Calcite precipitation#

Calcite precipitation can be described as

\(Ca^{2+} + CO_3^{2-} \rightarrow CaCO_3(s)\)

The rate expression is

\(r = S \cdot k \cdot (1 - \displaystyle\frac{Q}{K_{sp}})\)

where \(S\) is the reactive surface area, \(k\) is the intrinsic rate constant, \(Q\) is the ion activity product, and \(K_{sp}\) is the solubility constant of calcite.

Problem Specification#

Flow and transport#

The domain is a 2D dimensional rectangle, 60x50 cm in size. Material properties are homogeneous in the domain:

  • Porosity = 0.38

  • Hydraulic conductivity = 0.38 cm/s

The inlet face is divided in two equal halves. The top half is subject to the following conditions:

  • flow rate = 0.50 cm/s

  • \([Ca^{2+}] = 0.05 M\)

The bottom half is subject to the following conditions:

  • flow rate = 0.26 cm/s

  • \([CO_3^{2-}] = 0.05 M\)

The initial concentration of all species in the domain is \(10^{-10} M\)

The dispersion coefficients for longitudinal and transverse component (relative to the local velocity vector) are:

  • \(\alpha_{L} = \alpha_{T} = 0.0001 m\)

The molecular diffusivities for all species are zeros.

Geochemistry#

The calcite mineral surface area is:

  • \(S = 250 \text{ m}^2 \text{/m}^3\)

While the instrinsic rate constant for calcite dissolution is:

  • \(k = 10^{-11} \text{ mol/cm}^2 \text{s}\)

With calcite solubility being:

  • \(\text{log}(K_{sp}) = -8.4801\)

Results and Comparison#

Expected results#

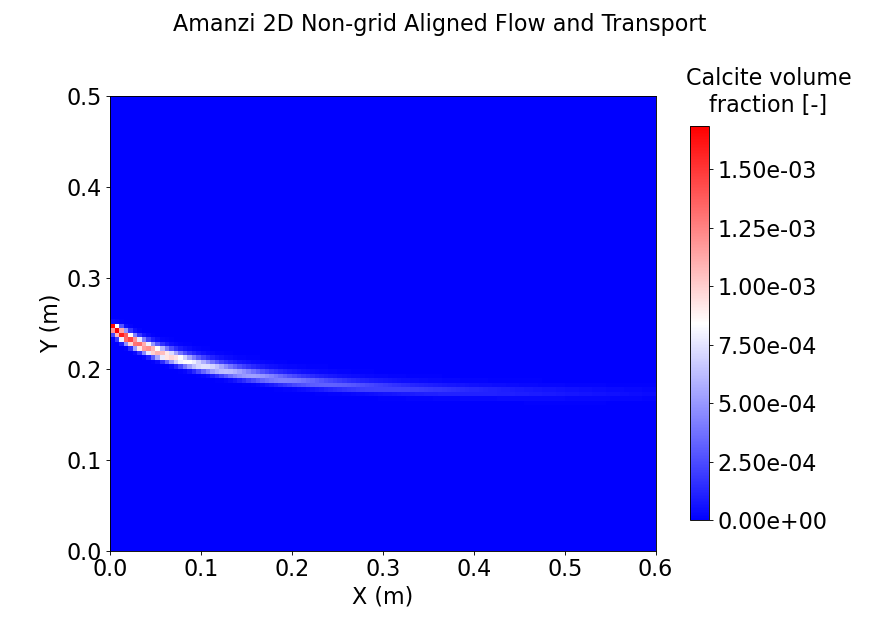
Precipitation of calcite is expected to occur in the zone where the two solutions mix. Because the flow rate in the top half is faster, the mixing zone curves downwards, into the bottom half of the domain. Since the precipitation of calcite is fast relative to transport, the mixing zone is narrow; the effective reaction rate is transport-limited. We do not have an analytic solution for this problem. Due to the discontinuous boundary condition, we cannot expect formal convergence of either the structured AMR or unstructured algorithms to their second-order design rate. However, we anticipate a robust, monotonic solution with minimal cross-stream diffusion/dispersion.

Simulation results#

Simulation results show a good agreement with expected results. Precipitation of calcite is indicated by its volume fraction at time 72 seconds (see Figure). For the structured and unstructured discretizations, the solution profiles for the precipitated calcite are similar narrow bands between the inflowing solutes. In both case, the solute profiles are monotonic and well-behaved at all mesh resolutions. With additional refinement (not shown), the magnitude of the peak calcite volume fraction increases (due the increased vertical gradients of precipitating solutes at the inflow boundary condition), but its concentration stays properly confined to a narrow zone at the interface. These results demonstrate that Amanzi is capable of robustly capturing non-grid-aligned processes in both the structured and unstructured mesh frameworks.

(Source code, png, hires.png, pdf)

../../../_images/non_grid_aligned.png

References#

[Bar94]

T. Barth. Aspects of unstructured grids and finite-volume solvers for the euler and navier-stokes equations. Lecture Notes presented at VKI Lecture Series, 1994.

[BDS88]

J.B. Bell, C.N. Dawson, and G.R. Shubin. An unsplit higher order godunov method for scalar conservation laws in multiple dimensions. J. Comput. Phys., 74:1–24, 1988.

[dVLM14]

L. Beirao da Veiga, K. Lipnikov, and G. Manzini. The Mimetic Finite Difference Method for Elliptic PDEs. Springer, 2014.

[NMAB11]

A. Nonaka, S. May, A. S. Almgren, and J. B. Bell. A three-dimensional, unsplit godunov method ofr scalar conservation laws. SIAM J. Sci. Comput, 33(4):2039–2062, 2011.

[TRL+08]

A. M. Tartakovsky, G. Redden, P. C. Lichtner, T. D. Scheibe, and P. Meakin. Mixing-induced precipitation: experimental study and multiscale numerical analysis. Water Resour. Res., 2008.

[YVWD12]

H. Yoon, A. J. Valocchi, C. J. Werth, and T. Dewers. Pore-scale simulation of mixing-induced calcium carbonate precipitation and dissolution in a microfluidic pore network. Water Resour. Res., 2012.

About#

  • Benchmark simulators: N/A

  • Files

    • Amanzi input file/s (native chemistry): non_grid_aligned-u.xml

    • Amanzi input file/s (Alquimia chemistry): non_grid_aligned-u-alq.xml, calcite_pflotran.in

  • Location: testing/benchmark/chemistry/non_grid_aligned_dispersion/

  • Author: K. Lipnikov, M. Day, S. Molins

  • Documentation: S. Molins

  • Created on: March 10, 2014